2022年考研数学大纲已经发布,比较今年的考试大纲与去年的考试大纲,我们发现在考研数学中高等数学的重点的内容和去年的几乎没有什么变化,往年的重要知识点在今年依然是考查的重点,当然也是我们学习的重点,需要我们必须要掌握的。其中一元函数导数的计算又是我们需要掌握的最基本的,最重要的知识点之一。在此,我们对这个知识点进行了总结与分析,帮助大家更好的复习。
(一)首先,我们从题型、考频、分值、难度值和区分度这几个角度帮助大家了解一元函数的导数的计算(如表1所示):
| 题型 | 考频 | 分值 | 难度值 | 区分度 | |
| 35年 | 初等函数的导数 | 18 | 63 | 0.574 | 0.445 |
| 隐函数导数 | 15 | 57 | 0.67 | 0.471 | |
| 参数方程的导数 | 17 | 84 | 0.691 | 0.53 | |
| 抽象函数的导数 | 9 | 42 | 0.549 | 0.469 | |
| 高阶导数 | 11 | 42 | 0.374 | 0.387 | |
| 近10年 | 初等函数的导数 | 3 | 13 | 0.606 | 0.427 |
| 隐函数导数 | 0 | 0 | 0 | 0 | |
| 参数方程的导数 | 4 | 17 | 0.665 | 0.538 | |
| 抽象函数的导数 | 1 | 4 | 0.5 | 0.469 | |
| 高阶导数 | 4 | 16 | 0.364 | 0.368 |
从上述表格不难发现,一元函数导数的计算这个知识点,涉及到的题型比较多样,共计五种题型。并且,近35年,直接考查本知识点一共70题,共计288分,小题为主,除了高阶导数的计算之外,难度值在0.6左右,属于比较简单的题目,区分度在0.5左右,区分度良好,说明这部分题目是必得分的题目。高阶导数的计算相对较难,区分度不大,说明对于所有考生而言,高阶导数的计算比较难。近十年来看,直接考查一元函数导数的计算一共12题,共计50分,还是小题为主,只是考查频率略有下降,但是,咱们考生要注意的是2021年数二有一道小题(5分)直接考查到这个知识点,所以考生们一定要学好这一部分,因为它不但会直接考查,而且还是后边知识的基础。
(二)其次,我们总结了解决一元函数导数的计算的方法(如图1所示):
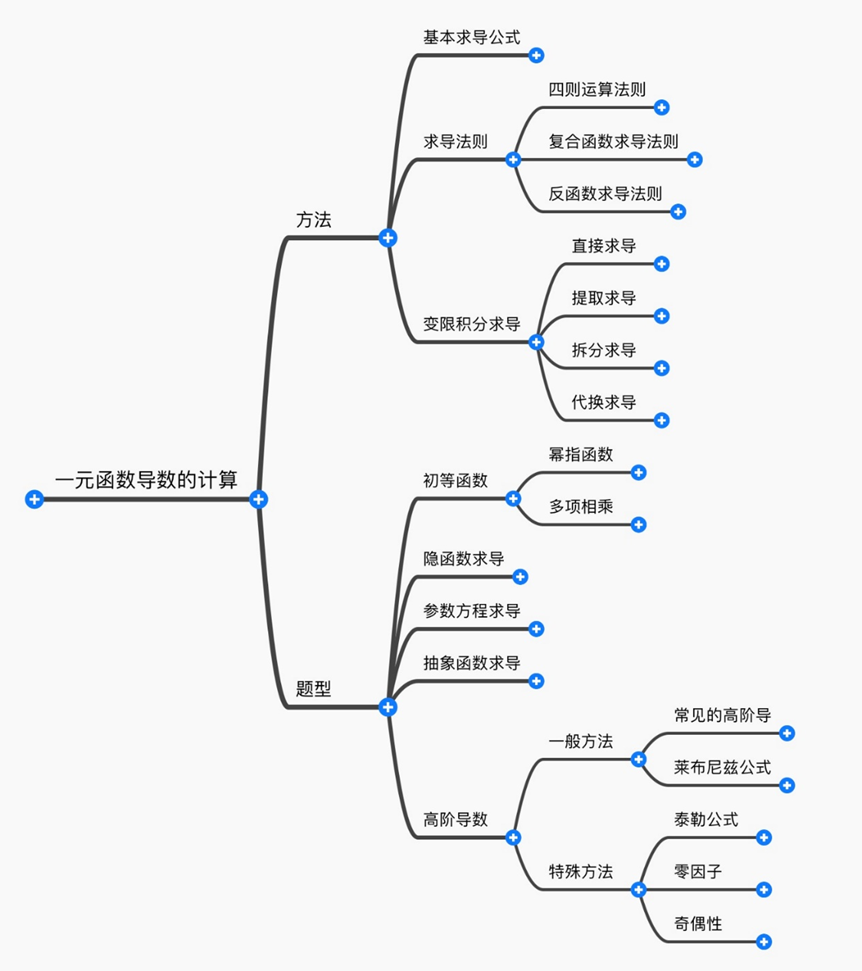
图1
如上图(图1)所示,考生不但需要掌握基本的求导方法,而且还要掌握解决不同的题型所需要的方法。
(三)具体题目

最后,考研数学大纲的发布,不但进一步明确了我们学习的方向,也在提醒各位考生,2022年研究生招生考试已经距离我们越来越近了,在此,希望大家能够做到戒骄戒躁,学习上一定要扎扎实实,在打好基础的同时,能够增强做题能力,加快做题速度,从而一步一个脚印的走向自己的理想学府。






