【经典题1】
大安化工厂拟购入一台新型设备,购价为160万元,使用年限10年,无残值。该方案的最低投资报酬率要求为12%(以此作为贴现率)。使用新设备后,估计每年产生现金净流量30万元。
要求:用内含报酬率指标评价该方案是否可行?
【经典题2】
现有甲、乙两个机床购置方案,所要求的最低投资报酬率为10%。甲机床投资额10 000元,可用2年,无残值,每年产生8000元现金净流量。乙机床投资额20 000元,可用3年,无残值,每年产生10 000元现金净流量。同:两方案何者为优?
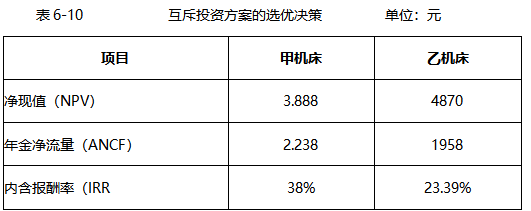
将两方案的期限调整为最小公倍数6年,即甲机床6年内周转3次,乙机床6年内周转2次。未调整之前,两方案的相关评价指标如表所示。
参考答案:
【解析一】
令:300000×年金现值系数-1600000=0
得:年金现值系数=5.3333
现已知方案的使用年限为10年,查年金现值系数表,可查得:时期10,系数5.333所对应的贴现率在12%~14%之间。采用插值法求得,该方案的内含报酬率为13.46%,高于最低投资报酬率12%,方案可行。
【解析二】
尽管甲方案净现值低于乙方案,但年金净流量和内含报酬率均高于乙方案。接两方案期限的最小公倍数测算,甲方案经历了3次投资循环,乙方案经历了2次投资循环。
各方案的相关评价指标为:
(1)甲方案。
净现值=8000×4.3553-10000×0.6830-10000×0.8264-10000
=9748(元)
年金净流量=9748/4.3553=2238(元)
(2)乙方案。
净现值=10000×4.3553-20000×0.7513-20000
=8527(元)
年金净流量=8527/4.3553=1958(元)
上述计算说明,延长寿命期后,两方案投资期限相等,甲方案的净现值9748元高于乙方案的净现值8527元,故甲方案优于乙方案。
至于内含报酬率指标,可以测算出:当i=38%时,甲方案净现值=0;当i=
23.39%时,乙方案净现值=0。这说明,只要方案的现金流量状态不变,接公倍数年限延长寿命后,方案的内含报酬率并不会变化。
同样,只要方案的现金流量状态不变,按公倍数年限延长寿命后,方案的年金净流量指标也不会改变。甲方案仍为2238元,乙方案仍为1958元。由于寿命期不同的项目,换算为最小公倍数年限比较麻烦,而接各方案本身期限计算的年金净流量与换算公倍数期限后的结果一致。因此,实务中对于期限不等的互斥方案比较,无须换算寿命期限,直接按原始期限的年金净流量指标决策。
综上所述,互斥投资方案的选优决策中,年金净流量全面反映了各方案的获利数额,是最佳的决策指标。净现值指标在寿命期不同的情况下,需要按各方案最小公倍期限调整计算,在其余情况下的决策结论也是正确的。







 中级会计实务
中级会计实务